신뢰구간을 구해보는 일을 하자!
데이터는...
2023.02.16 - [멋쟁이사자처럼 AI스쿨] - 통계 특강1
통계 특강1
하루에 100명이 고객이 구매율 30%로 365일 시뮬레이션을... 이항분포로 돌려보자! binom import! from scipy.stats import binom 이항분포로 100명, 구매율 0.3, 365일 데이터를 만들어보면... data = binom.rvs(n=100, p=0.
helpming.tistory.com
에서 많이 다뤄봤던 car데이터를 사용하자!
일단 pingouin을 설치해보자!
pip install pingouin
그리고 import해준다!
import pingouin as pg
ttest함수로 가격 평균의 95% 신뢰구간을 구해보자!
컬럼 1개에 대해 분석하므로 x에 가격컬럼, y에 0을 넣어줬다!
pg.ttest(df['price'], 0, confidence=0.95)
CI95%항목을 보면 신뢰구간을 확인할 수 있다!
이번엔 주행거리 평균의 99% 신뢰구간을 구해보자!
pg.ttest(df['mileage'], 0, confidence=0.99)
이렇다!
이번에는 모델이 아반떼인 경우 가격 평균의 95% 신뢰구간을 구해보자!
pg.ttest(df[df['model'] == 'Avante']['price'], 0, confidence=0.95)
모델이 K3인 경우 가격 평균의 95% 신뢰구간은...
pg.ttest(df[df['model'] == 'K3']['price'], 0, confidence=0.95)
이런데...
아반떼보다 K3 가격 평균이 높기 때문에 신뢰구간이 더 높게 잡힌 것을 알 수 있다!
이번에는 부트스트래핑을 통한 가격 평균의 95% 신뢰구간을 추정해보자!
spicy와 numpy를 import해주고...
stats의 bootstrap함수를 사용하면...
import scipy
import numpy as np
scipy.stats.bootstrap([df['price']], np.mean)stats의 bootstrap함수를 사용하면...

가격 평균의 신뢰구간이 구해지는데...
ttest랑 아주 조금 차이가 있다!
이번에는 가격 평균의 신뢰구간을 구해보는데 99999번 시뮬레이션을 해서 구해보면...
scipy.stats.bootstrap([df['price']], np.mean, confidence_level=0.95, n_resamples=99999)
아주 미세하기 구간이 좁혀졌다!
본격적인 가설검정을 해보자!
일단 개요를 보면...

이렇다!
가정먼저 독립표본 t검정(평균의 차이 비교)을 해보자!
가격평균 = 900이라는 귀무가설을 검정해보자!
pg.ttest(df['price'], 900)
p밸류가 유의수준(기본값 0.05) 보다 작기 때문에 귀무가설을 기각!
가격평균은 900이 아니다!
이번엔 가격평균 = 850 귀무가설을 검정해보면...
pg.ttest(df['price'], 850)
p밸류가 0.05보다 크기 때문에 귀무가설을 기각 못해서...
결론 유보!(가격평균이 850이 아니라고 할 수 없다!)
이번에는 아반떼와 K3의 가격 평균이 같다는 귀무가설을 검정해보자!
Avante = df[df['model'] == 'Avante']['price']
K3 = df[df['model'] == 'K3']['price']
pg.ttest(Avante, K3)
p밸류가 0.05보다 작기 때문에 귀무가설 기각!
아반떼와 K3 가격 평균에는 차이가 있다!
신뢰구간을 보고 해석해보면...
모집단에서는 아반떼 평균이 못해도 8만원 많으면 152만원 정도 싸다고 해석할 수 있다!
이번에는 만 휘트니 U 검정을 통해서...
아반떼와 K3의 가격 평균이 같다는 귀무가설을 검정해보자!
Avante = df[df['model'] == "Avante"]['price']
K3 = df[df['model'] == "K3"]['price']
pg.mwu(Avante, K3)
p밸류가 0.05보다 작기 때문에 귀무가설 기각...
만 휘트니 U 검정을 통해서도 아반떼와 K3 가격 평균에는 차이가 있다!
이번엔 효과크기 중 하나인 에타제곱(변수가 평균을 다르게 만드는데 얼마나 기여하는지)을 알아보자!
에타제곱은 anova검정과 compute_effsize를 통해 구할 수 있는데...
먼저 anova를 통해 아반떼랑 K3 모델 차이가 가격에 얼마나 기여하는지 알아보면...
pg.anova(dv='price', between='model', data=df)
np2 항목을 보면 되는데...
중고차마다 가격이 다 다른데, 그게 아반떼 또는 K3라서 다른 부분은 1.1% 밖에 안된다고 볼 수 있다!
이번엔 compute_effsize로 알아보면...
pg.compute_effsize(Avante, K3, eftype='eta-square')
1.4% 정도 가격차이에 기여를 한 것을 알 수 있다!
이번엔 cohen의 효과크기를 계산해보면...
pg.compute_effsize(Avante, K3, eftype='cohen')
음수가 나와서 모델차이는 오히려 가격 효과에 오히려 반대영향을 조금 준 것으로 나온다?
이번에는 대응표본 t검정(차이의 평균을 비교)을 해보자!
데이터는 남편과 아내의 가사노동 데이터로 해보자!
cp = pd.read_excel('data/couple.xlsx')
cp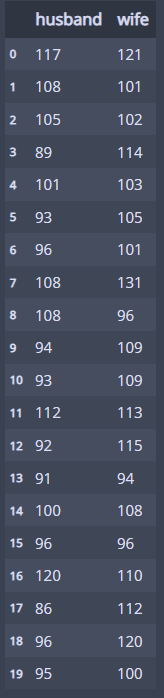
이런 데이터이다!
남편과 아내의 가사노동 시간이 쌍이니 대응표본 t검정을 하자!
x에 남편, y에 아내, paired=True를 해준다!
pg.ttest(cp['husband'], cp['wife'], paired=True)
귀무가설과 기각여부를 정리해보면....
- 귀무가설: 차이의 평균 = 0(남편과 아내가 가사노동시간이 같다)
- p = 0.007578 < 0.05 (귀무가설 기각)
즉, 남편과 아내의 가사노동시간이 다르다!
다음은 분산분석!
분산분석은 3가지 단계로 검정을 한다!
1. 등분산검정
- 분산이 같은지 검정
2. 분산분석
- 분산이 같으면 anova, 다르면 welch_anova
3. 사후검정
- 분산분석에서 귀무가설 기각 못하면 결론유보
- 기각 하면 분산이 같을 때 pairwise_tukey, 다를 때 pairwise_gameshowell
그럼 분산분석을 hr데이터를 사용해서 해보자!
hr = pd.read_excel('data/hr.xlsx')
hr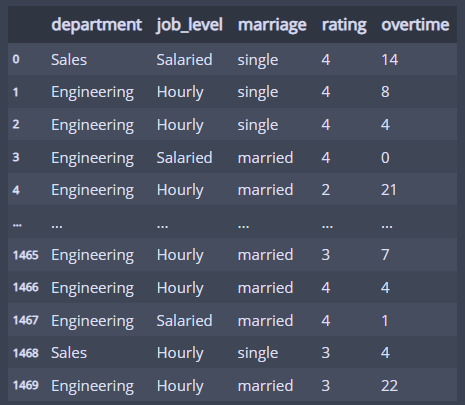
직원들의 데이터 같다!
job_level에 따른 rating에 대해 분산분석을 할 거라서...
job_level이 몇 집단인지 확인해보면...
hr['job_level'].unique()
Salaried, Hourly, Manager 총 세 집단에 대해 평균을 비교해보자!
1. 등분산성 검정
pg.homoscedasticity(dv='rating', group='job_level', data=hr)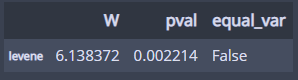
분산이 다르다!
2. 분산분석
분산이 다르므로 welch_anova로 분산분석을 해보자!
귀무가설은 세 집단의 rating 평균이 모두 같다!이다.
pg.welch_anova(dv='rating', between='job_level', data=hr)
p = 5.394990e-54 < 0.05 이므로 귀무가설 기각!
어떤 집단의 평균은 다르다!
3. 사후검정
어느 집단간 평균이 다른지 확인하기 위해 사후검정을 실시하는데...
등분산성 검정에서 분산이 다르므로... pairwise_gameshowell을 사용해 검정하자!
pg.pairwise_gameshowell(dv='rating', between='job_level', data=hr)
모든 집단 사이의 p값이 0.05보다 작으므로...
세 집단의 평균은 모두 다르다!
이번에는 liar 데이터를 가지고 분산분석을 해보자!
liar = pd.read_excel('data/liar.xlsx')
liar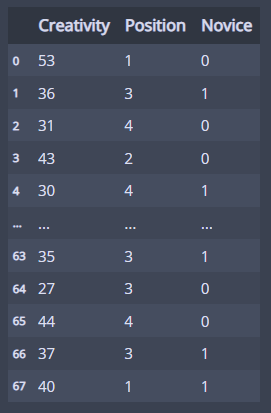
이런 데이터이다...
Position별로 Creativity의 평균이 다를까 분석해보자!
liar['Position'].unique()
총 6개 집단이다.
1. 등분산성 검정
pg.homoscedasticity(dv='Creativity', group='Position', data=liar)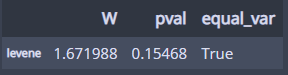
분산이 같다!
2. 분산분석
분산이 같으므로 anova로 분석!
pg.anova(dv='Creativity', between='Position', data=liar)
p = 0.000887 < 0.05이므로 모든 집단의 평균이 같다는 가설 기각!
=> 어떤 집단의 평균이 다르다!
3. 사후검정
등분산성 검정에서 분산이 같다고 했으므로 pairwise_tukey로 검정!
pg.pairwise_tukey(dv='Creativity', between='Position', data=liar)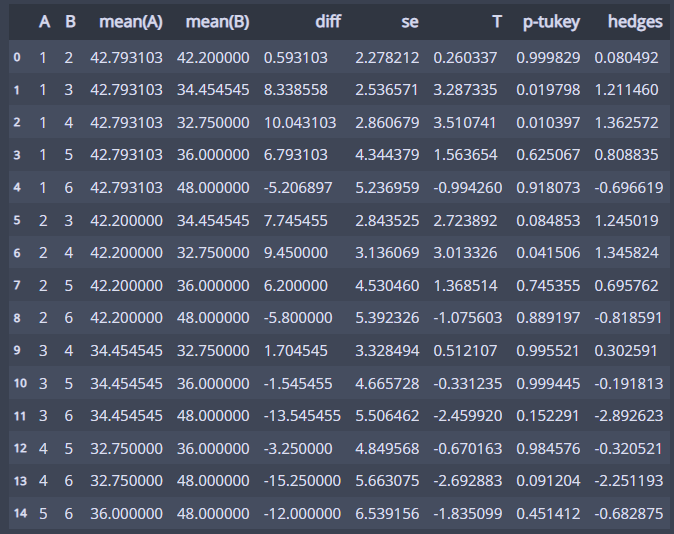
원하는 2개 집단 간에 평균이 다른지 확인할 수 있다!
'멋쟁이사자처럼 AI스쿨' 카테고리의 다른 글
| 통계 특강4 (2) | 2023.03.01 |
|---|---|
| 통계 특강3 (2) | 2023.03.01 |
| 통계 특강1 (0) | 2023.02.16 |
| 멋쟁이사자처럼 AI스쿨 8주차 회고 (0) | 2023.02.09 |
| 멋쟁이사자처럼miniproject2(행복지수와 코로나확진률) (0) | 2023.02.08 |




댓글