
저번 시간에는 연속형 변수에 대해서 검정해봤다!
이번에는 범주형에 대해서 검정해보자!
카이제곱 적합도 검정을 해보자!
먼저 카이제곱을 import 해주고...
from scipy.stats import chisquare
상황을 가정해보자!
50명에게 A, B 두 브랜드 선호도 조사를 했는데...
A브랜드를 선호하는 사람이 31명, B를 선호하는 사람이 19명 이라고 하자!
귀무가설 : 두 브랜드에 차이가 없다!(A 25명, B 25명)
카이제곱 검정을 해보면...
chisquare([31, 19], [25, 25])
p-value가 0.05보다 크므로 기무가설을 기각할 수 없다!
결국 두 브랜드 선호에 차이가 없다고 볼 수 있다!
50명에게 물어봐서 31:19 정도로는 두 브랜드 선호도 차이를 알 수 없는 것이다!
그럼 100명으로 늘려서 62명이 A를 선호, 38명이 B를 선호한다고 가정해보자!
귀무가설 : 두 브랜드에 차이가 없다!(A 50명, B 50명)
chisquare([62, 38], [50, 50])
이번에는 p-value < 0.05이므로...
귀무가설 기각!
두 브랜드 선호도에 차이가 있다고 볼 수 있다!
100명에게 물어봐서 62:38(31:19) 정도면 두 브랜드 선호도 차이가 있다!
이 두 사례로 표본의 크기의 중요성을 알 수 있다!
이번에는 hr데이터로 카이제곱 독립성 검정을 해보자!
hr = pd.read_excel('data/hr.xlsx')
hr
앞 시간에 사용했던 직원 데이터이다!
피벗 테이블 기능으로 결혼여부, 부서종류별 사람수를 세어보자!
hr.pivot_table(index='marriage', columns='department', aggfunc='size')
엔지니어링, 세일즈 부서는 싱글이 많고...
파이낸스 부서는 기혼자가 많다!
pingouin을 import하고
import pingouin as pg독립성 검정을 해보자!
expected, observed, stats = pg.chi2_independence(x='department', y='marriage', data=hr)
stats
stats를 확인해 보면 이렇다!
기대값은 이렇고...
expected
관찰값은...
observed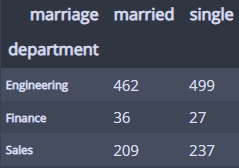
아까 피벗테이블로 확인한 값과 같다!
아주 자세하게 배운 것은 아니라서... 요정도만...
이번에는 맥니마 검정을 해보자!
우선 statsmodels설치하고...
!pip install statsmodels
50명에게 한 브랜드의 선호도 조사를 했는데...
40명이 불호, 10명이 호였다!
브랜드의 행사를 하고 다시 조사했더니
30명이 불호, 20명이 호였다!
이때 귀무가설은 브랜드 선호도가 행사 전 후에 차이가 있다! 이다.
맥니마 검정을 해보면...
from statsmodels.stats.contingency_tables import mcnemar
table = [[40, 10], [20, 30]]
m = mcnemar(table, exact=False, correction=False)
print(m)
p값이 0.05보다 크므로 귀무가설을 기각 못해서...
결론은 행사가 소용이 없었다...
그럼 이번에는 비율은 그대로 하고 100명으로 늘려서 검정해보자!
table = [[80, 20], [40, 60]]
m = mcnemar(table, exact=False, correction=False)
print(m)
이번에는 p값이 0.05보다 작으므로 귀무가설 기각!
행사 전 후에 차이가 있었다!... 즉, 행사가 효과가 있었다고 볼 수 있다!
'멋쟁이사자처럼 AI스쿨' 카테고리의 다른 글
| 통계 특강5 (0) | 2023.03.02 |
|---|---|
| 통계 특강4 (2) | 2023.03.01 |
| 통계 특강2 (2) | 2023.03.01 |
| 통계 특강1 (0) | 2023.02.16 |
| 멋쟁이사자처럼 AI스쿨 8주차 회고 (0) | 2023.02.09 |




댓글