하루에 100명이 고객이 구매율 30%로 365일 시뮬레이션을...
이항분포로 돌려보자!
binom import!
from scipy.stats import binom
이항분포로 100명, 구매율 0.3, 365일 데이터를 만들어보면...
data = binom.rvs(n=100, p=0.3, size=365) # 100명의 고객, 30% 구매율, 365일 시뮬레이션
data
이렇게 된다!
이것을 히스토그램으로 그려보자!
import matplotlib.pyplot as plt
plt.hist(data, bins=40, range=[10, 50]);
손님이 가장 적게오는 날은 18명, 가장 많이오는 날은 46명이고...
구매율이 30%라 30명 주변에 몰려있는 것을 볼 수 있다!
확률밀도함수로 딱 40명이 구매할 확률을 보자!
binom.pmf(k=40, n=100, p=0.3)
0.85%정도이다!
누적분포함수로 0명 부터 30명까지 구매할 확률을 보자!
binom.cdf(k=30, n=100, p=0.3)
55퍼정도이다!
pdf로 0명 부터 100명까지 구매학률을 보면...
import numpy as np
x = np.arange(0, 101)
p = binom.pmf(k=x, n=100, p=0.3)
plt.plot(x, p)
plt.xlabel('k');
30에서 가장 높은 형태이다!
cdf로 보면...
p = binom.cdf(k=x, n=100, p=0.3) # 누적
plt.plot(x, p)
plt.xlabel('k');
이렇다!
카카오톡에서 서버 10000개가 있는데 9800대가 가동되어야 괜찮다고 가정해보자!
1대가 고장날 확률은 0.01이다.
그럼 정상적으로 돌아갈 확률은 어떻게 될까?
cdf를 통해 구해보면...
binom.cdf(k=200, n=10000, p=0.01)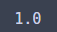
1이다. 평생 걱정 없을 것이다...
그럼 50대를 팔아보자!
binom.cdf(k=150, n=9950, p=0.01)
이정도 괜찮을 것 같다!
10대를 더 팔아보면...
binom.cdf(k=140, n=9940, p=0.01)
2만분의 1 이하의 확률이다!
이정도도 괜찮을 것 같으니...
총 60개를 팔아서 과자사먹자!
이번에는 정규본포로 100명, 구매율 0.3, 365일 데이터를 만들어보자!
m = 100 * 0.3
s = np.sqrt(100 * 0.3 * 0.7)
data = norm.rvs(loc=m, scale=s, size=365)이렇게 데이터를 만들고 히스토그램을 그려보면...
plt.hist(data, bins=40, range=[10, 50]);
이항분포로 그린 것과 유사하다!
정규분포로 사람이 30명 까지 올 확률을 cdf로 확인해 보면...
norm.cdf(x=30, loc=m, scale=s)
딱 절반이다!
이항분포로 따지면...
# 이항분포로 따졌을 때
binom.cdf(k=30, n=100, p=0.3)
0.5보다 조금 큰데...
이번엔 하루에 만명이 0.3의 확률로 구매한다고 치자!
먼저 정규분포로보면...
norm.cdf(x=3000, loc=10000*0.3, scale=10000*0.3*0.7)
딱 절반이고...
이항분포로 보면...
norm.cdf(x=3000, loc=10000*0.3, scale=10000*0.3*0.7)
절반에 가까운 수치이다!
이것을 통해 n을 키우면 키울수록 정규분포에 근사하는 것을 알 수있다!
car 데이터를 보자!
import pandas as pd
df = pd.read_excel('data/car.xlsx')
df
탄 거리, 모델, 가격, 년도, 차가 받은 데미지, 다른 차한테 준 데미지 컬럼이 있는 데이터이다!
데이터를 조사해보자!
먼저 가격의 평균!
df['price'].mean()
가격의 중앙값!
df['price'].median()
모델이 몇 종류이고 각각 몇개인지!
df['model'].value_counts()
아반때가 3배? 정도 많다!
마일리지의 평균과 중앙값!
df['mileage'].mean(), df['mileage'].median()
내 차가 받은 데미지의 평균과 중앙값!
df['my_car_damage'].mean(), df['my_car_damage'].median()
내 차가 준 데미지의 평균과 중앙값!
df['other_car_damage'].mean(), df['other_car_damage'].median()
가격 의 최소값과 최대값!
df['price'].min(), df['price'].max()
가격의 범위
df['price'].max() - df['price'].min()
가격의 IQR
df['price'].quantile(.75) - df['price'].quantile(.25)
데이터를 요정도로 살펴봤다!
시각화로도 한번 데이터를 살펴보자!
boxplot으로 가격의 분포를 보면...
import seaborn as sns
sns.boxplot(data=df, x='price');
높은 쪽이 편차가 심하다!
모델별로 가격의 분포를 보면...
sns.boxplot(data=df, x='price', y='model');
아반떼가 더 넓게 분포해있다!
마일리지의 분포도 보자!
sns.boxplot(data=df, x='mileage');
몇몇 차가 정말 많이 탔다!
마일리지의 분산과 표준편차를 보면...
df['mileage'].var(), np.sqrt(df['mileage'].var())
이렇다!
히스토그램으로 가격의 분포를 보자!
sns.histplot(data=df, x='price');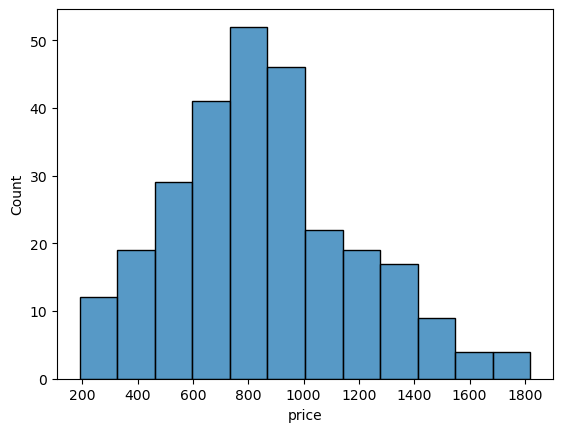
살짝 가격이 싼 쪽에 몰려있다!
막대기를 좀 작게해서도 보자!
sns.histplot(x='price', data=df, bins=[0, 500, 1000, 1500, 2000, 2500]);
이번엔 막대기 개수를 30개로 하고 커널밀도추정도 추가해보자!
sns.histplot(data=df, x='price', bins=30, kde=True);
이렇게 매끄러운 선인 커널밀도추정도 들어간다!
이번엔 hiring 데이터를 보자!
hiring = pd.read_excel('data/hiring.xlsx')
hiring
학점, 테스트, 전공비전공유무, 고용여부 등이 나와있는 데이터이다!
일단 info()를 확인해보면...
hiring.info()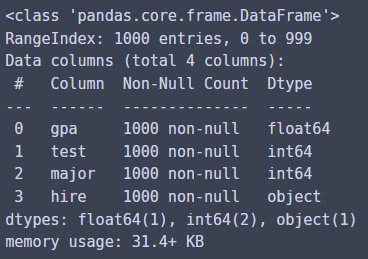
결측치는 없고 4개의 열과 1000행을 가진 데이터이다!
이번엔 hire에 뭐가 얼마나 있는지 보면...
hiring['hire'].value_counts()
F는 507개 P는 493개가 있다!
전공 유무는...
hiring['major'].value_counts()
전공한 사람이 500명 전공 안한사람이 500명이다!
학점의 평균과 중앙값도 보자!
hiring['gpa'].mean(), hiring['gpa'].median()
평균이 살짝? 높다!
test의 IQR은...
iqr = hiring['test'].quantile(0.75) - hiring['test'].quantile(0.25)
iqr
요정도! 이다
gpa의 히스토그램을 그려보면...
sns.histplot(data=hiring, x='gpa');
중간에 많이 모여있다!
박스플롯으로 test의 분포를 그려보면...
sns.boxplot(data=hiring, y='test');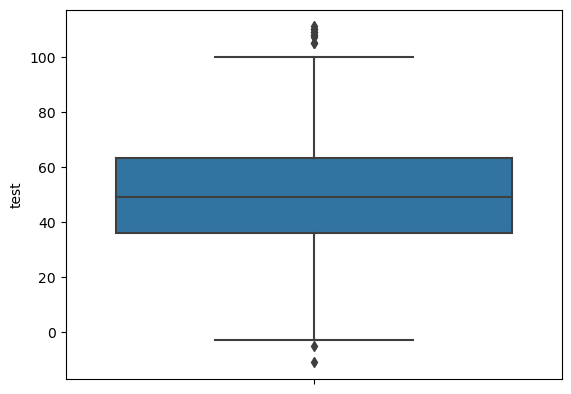
이렇게 몇몇 점이 밖에 찍혀있다!
몇 개가 찍혀있는지 IQR과 Q1, Q3로 계산해보면...
lowerbound = hiring['test'].quantile(0.25) - 1.5 * iqr
upperbound = hiring['test'].quantile(0.75) + 1.5 * iqr
len(hiring[(hiring['test'] > upperbound) | (hiring['test'] < lowerbound)])
12개의 점이 밖에 찍혀있다!
'멋쟁이사자처럼 AI스쿨' 카테고리의 다른 글
| 통계 특강3 (2) | 2023.03.01 |
|---|---|
| 통계 특강2 (2) | 2023.03.01 |
| 멋쟁이사자처럼 AI스쿨 8주차 회고 (0) | 2023.02.09 |
| 멋쟁이사자처럼miniproject2(행복지수와 코로나확진률) (0) | 2023.02.08 |
| 멋쟁이사자처럼 AI스쿨 7주차 회고 (0) | 2023.02.02 |




댓글