강사님이 seaborn내장 데이터셋인 diamonds로...
간단한 eda와 시각화 과제를 내주셨는데...
과제가 생각보다 일찍 끝나서...
간단히? 통계 분석을 해봤다!
우선 필요라이브러리 로드!
import pandas as pd
import seaborn as sns
import matplotlib.pyplot as plt
import plotly.express as px
import numpy as np
%config InlineBackend.figure_format = 'retina'
%matplotlib inline
데이터는 diamonds데이터인데...
53940개의 다이아몬드 정보를 담고 있다!(결측치는 없음)
df = sns.load_dataset("diamonds")
print(df.shape)
df.head()
약간의 전처리를 통해
가격이 900보다 작은 값은 low
5000보다 큰 값은 high
나머지는 medium으로... 해준...
category컬럼도 전처리로 생성해줬다...
df.loc[df['price'] < 900, 'category'] = 'low'
df.loc[df['price'] > 5000, 'category'] = 'high'
df['category'] = df['category'].fillna('medium')
df
이제 본격적인 통계분석 시작해보자!
그럼 pingouin을 import해주고...
import pingouin as pg
수치형 변수 기술통계 확인!
df.describe()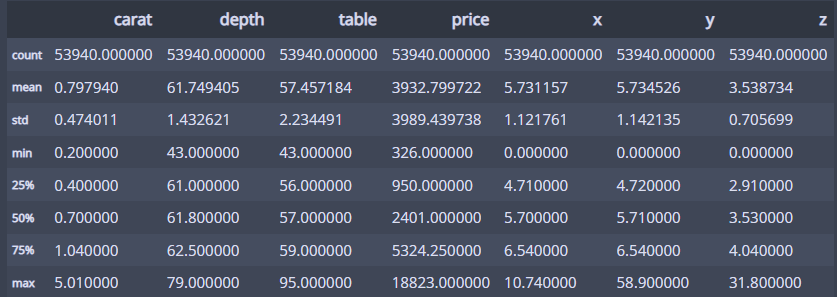
범주형(여기서는 category형이다!) 변수 기술통계 확인!
df.describe(include='category')
먼저 가설검정을 해보자!
위의 기술통계에서 price의 평균이 3932.799722이니까...
price가격 평균=4000이라는 귀무가설을 검증해보자!
pg.ttest(df['price'], 3900)
p값이 0.05보다 작기 때문에 귀무가설 기각! 가격 평균은 4000이 아니다!
이번엔 3932로 해보자!
pg.ttest(df['price'], 3932)
p값이 0.05보다 크기 때문에 결론유보! 가격 평균은 3932와 다르다고 할 수 없다!
또 기술 통계에서 본 캐럿 평균이 0.797940이니까...
캐럿 평균 = 0.8 이라는 귀무가설을 검증해보자!
pg.ttest(df['carat'], 0.8)
p값이 0.05보다 크기 때문에 결론유보! 캐럿 평균은 0.8과 다르다고 할 수 없다!
효과크기를 살펴볼건데...
에타제곱을 통해 cut이 가격에 얼마나 기여하는지 알아보면...
pg.anova(dv='price', between='cut', data=df)
np2를 확인해보면 약 1.3%정도 기여한다...
이번엔 carat이 가격에 얼마나 기여하는지 알아보면...
pg.anova(dv='price', between='carat', data=df)
87% 기여한 것을 보면 역시 다이아몬드는 캐럿빨인가...? 싶다!
이번엔 분산분석을 해보자!
clarity에 따른 가격 평균의 차이를 알아볼 것이다...
일단 범주의 개수를 알아보면...
df['clarity'].unique()
일단 범주는 8개이다!
1. 등분산검정(귀무가설 : clarity별 분산이 같다!)
pg.homoscedasticity(dv='price', group='clarity', data=df)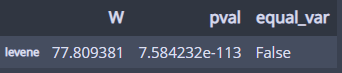
분산이 다르다!
2. 분산분석(분산이 다르므로 welch_anova)
귀무가설 : 모든 clarity 가격 평균이 같다!
pg.welch_anova(dv='price', between='clarity', data=df)
pvalue가 0.05보다 작으므로 가설 기각, 어떤 clarity의(하나라도) 가격 평균이 다르다!
3. 사후검정(어떻게 다른지... 분산이 다르므로 pairwise_gameshowell사용)
pg.pairwise_gameshowell(dv='price', between='clarity', data=df)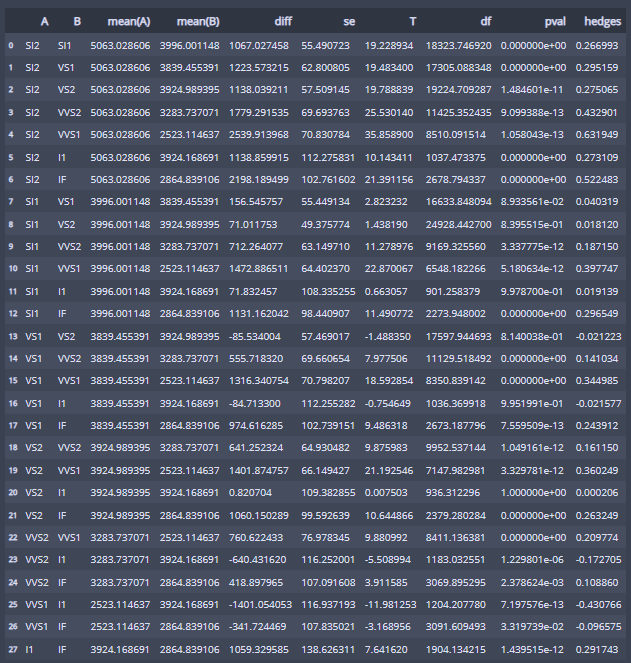
관심 있는 clarity 사이에 가격 평균 차이가 있는지 p_value를 통해 확인해 보면 된다!
예를 들어 22행을 보면 VS1과 VS2의 pvalue는 8.140038e-01 = 0.8140039 > 0.05이므로 가격 차이가 없다고 볼 수 있다!
이번에는 color별 가격 평균의 차이를 분산분석해보자!
df['cut'].unique()
범주 5개이다!
1. 등분산 검정
pg.homoscedasticity(dv='price', group='cut', data=df)
분산이 다르다!
2. 분산분석(분산이 다르므로 welch_anova)
귀무가설 : 모든 cut의 가격 평균이 같다!
pg.welch_anova(dv='price', between='cut', data=df)
p < 0.05이므로 귀무가설 기각.. 어떤 cut의 가격 평균이 다르다!
3. 사후검정(어떻게 다른지... 분산이 다르므로 pairwise_gameshowell사용)
pg.pairwise_gameshowell(dv='price', between='cut', data=df)
나머지는 가격 평균의 차이가 있고(p < 0.05)
Fair vs Preminum, Good vs Very Good 정도는 차이가 없다고 볼 수 있겠다!(p > 0.05)
이번엔 상관분석!
전체 수치형 변수의 상관계수를 확인해보면...
df.corr()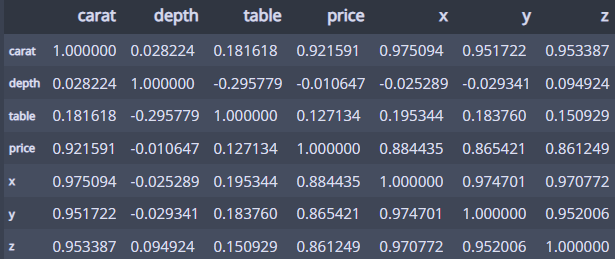
역시 가격과 관련이 가장 많은 변수는 캐럿이다!
캐럿과 가격의 산점도를 그려볼 것인데...
다른 정보도 함께 추가해서 보면 좋을 것 같다는 생각에...
범주형인 clarity를 확인해봤다!

출처 : https://www.tiffany.kr/engagement/the-tiffany-guide-to-diamonds/clarity/
다이아몬드 투명도: 교육 & 투명도 차트 | Tiffany & Co.
다이아몬드 투명도는 현미경으로 10배 확대했을 때 보이는 다이아몬드의 순도와 희소성에 대한 측정기준입니다. 컷은 다이아몬드의 패싯이 빛과 상호작용하는 방식에 따라 결정되며, 대칭, 비
www.tiffany.kr
IF > VVS1, VVS2 > VS1, VS2 > SI1, SI2 > I1 순으로 등급이 높아보이는데...
투명도가 다르니까 캐럿별 가격 차이 보다 캐럿별 가격차이를 투명도와 함께 보면 괜찮을 것이라는 생각!
plt.figure(figsize=(8, 8))
sns.scatterplot(x='carat', y='price', hue='clarity', data=df);
확실히 carat과 price는 양의 상관관계임을 확인해 볼 수 있고...
투명도가 높으면 같은 캐럿 내에서 가격이 비싼 것을 시각적으로 확인!
또 캐럿이 클수록 투명도가 떨어지고 투명도가 떨어질수록 캐럿이 큰 것도 확인할 수 있다!
이번엔 관계가 별로 없는 것도 산점도로 확인해보자!
상관행렬을 보면 depth랑 price의 상관관계가 약해보인다
sns.scatterplot(x='depth', y='price', data=df);
무슨 태풍 처럼 그려진 모습...(거의 상관이 없다!)
마지막으로 회기분석!
최소제곱법으로 회기분석을 해보자!
가격을 종속변수로 하고 캐럿을 독립변수로 해보자!
from statsmodels.formula.api import ols # ols:최소제곱법
m_carat = ols('price ~ carat', df).fit()
m_carat.summary()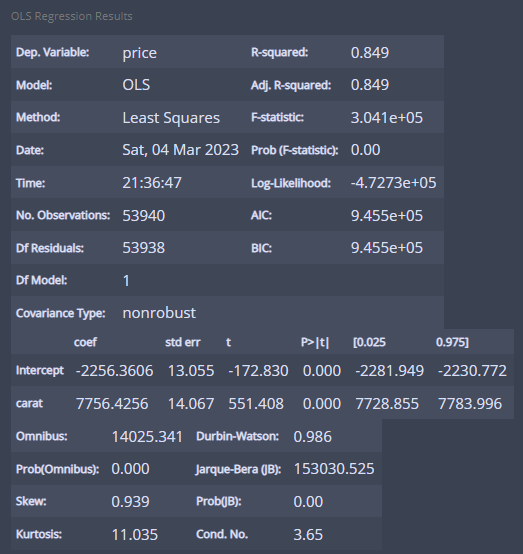
정보가 이렇게 나오는데...
자세히 살펴보면...

R제곱(R-squared를 보면...) 0.849로 설명력이 많이 높다!
즉 캐럿이 가격 분산의 84.9%를 설명한다고 볼 수 있다!

intercept = -2256.3606으로 0캐럿일 때 가격을 의미한다!
그리고 carat = 7756.4256을 보면 1캐럿이 증가할 때마다 가격이 7756.4256증가한다!
p = 0.000 < 0.05이므로 귀무가설 기각...(귀무가설 : 기울기(carat=0))
즉, 유효한 모형이다!
regplot으로 산점도와 함께 예측모형을 그려보자!
plt.figure(figsize=(8,8))
sns.regplot(x='carat', y='price', data=df);
이렇게 그려진다!
한번 carat만 가지고 가격을 예측해 볼건데...
my_diamonds = pd.DataFrame({'carat':[3, 4]})
my_diamonds
이렇게 3캐럿, 4캐럿짜리 다이아몬드를 만들어서... 예측해보면...
m_carat.predict(my_diamonds)
아주 비싼 가격이다...
이번에는 cut으로 회기분석해보자!(독립변수가 범주형 : 더미 코딩)
m_clarity = ols('price ~ clarity', df).fit()
m_clarity.summary()
정보가 이렇게 나오는데...
자세히 보면...

일단 R제곱은... 0.027로 clarity가 가격 분산의 2.7%를 설명한다!
모형 분석을 해보자면...

모형 분석을 해보면...
y= 2864.8391-341.7245*clarity[VVS1]
+418.8980*clarity[VVS2]
+974.6163*clarity[VS1]
+1060.1503*clarity[VS2]
+1131.1620*clarity[SI1]
+2198.1895*clarity[SI2]
+1059.3296*clarity[I1]
이런 식이고...
해석해보면...(더미코딩으로 해석)
IF는 모든 clarity에 0을 대입(더미코딩) 따라서 가격이 2864.8391이고...
VVS1는 clarity[VVS1]에만 1을 넣어주고 나머지는...0대입해서 => 2864.8391 - 341.7245 = 2523.1146000000003의 가격...
VVS2는 clarity[VVS2]만 1대입 나머지는 0 => 2864.8391 + 418.8980 = 3283.7371000000003의 가격...
이렇게 모든 clarity 별로 계산할 수 있다....
아까 IF > VVS1, VVS2 > VS1, VS2 > SI1, SI2 > I1 순의 둥굽안데 가격이 오히려 반대의 경향을 띄는 것은...
=> carat을 고려하지 않은 clarity만 고려해서 그렇다(산점도로 보면 carat이 클수록 clarity는 낮은 경향)
실제로 확인해 보면 clarity 등급이 높은 순으로 캐럿의 평균이 작은 것을 확인할 수 있다!
df.groupby('clarity').agg({'carat':'mean'})
이번에는 캐럿을 통제하고 clarity를 를 보자!
m_carat_clarity = ols('price ~ carat + clarity', df).fit()
m_carat_clarity.summary()
carat을 통제하고 clarity를 보면 확실히 clarity 등급이 높을수록 비싼 경향을 확인할 수 있다!
그리고 R제곱이 0.895로 캐럿만 봤을 때(0.849) 보다 상승 => 더 정확한 모델임을 알 수 있다!
아까 분산분석에서 cut별로 가격 평균이 다른 것을 확인했으니... cut도 넣어서 모델을 만들어보면..
m_carat_clarity_cut = ols('price ~ carat + clarity + cut', df).fit()
m_carat_clarity_cut.summary()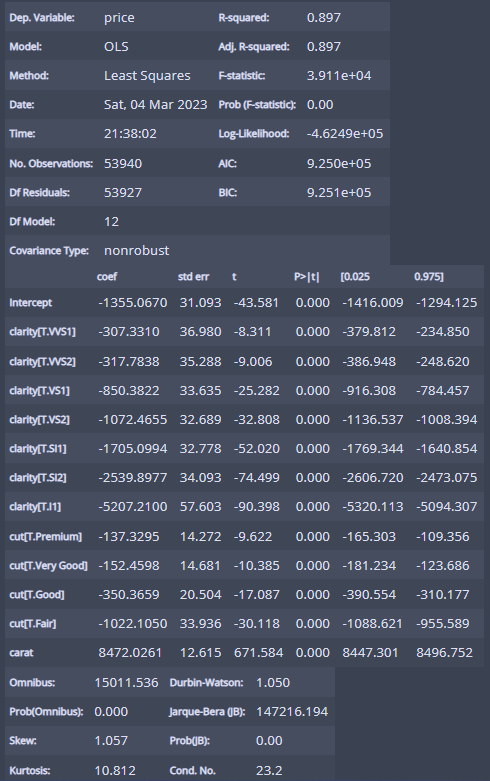
R제곱이 0.897로 미세하기 오르긴 올랐다!
이 모델로 내 다이아몬드를 예측해보자!
my_precious = pd.DataFrame({'carat':[3],
'clarity':['IF'],
'cut':['Ideal']})
my_precious
3캐럿짜리 완전 최상급 프로포즈용 반지에 쓰일 다이아몬드를 만들어버린...
암튼 예측해보면...
m_carat_clarity_cut.predict(my_precious)
데이터에있는 최고가 다이아몬드보다 비싸다...!
df['price'].max()
여기까지 재미로 통계분석을 해봤다...
'멋쟁이사자처럼 AI스쿨' 카테고리의 다른 글
| 멋쟁이사자처럼 AI스쿨 13주차 회고 (0) | 2023.03.16 |
|---|---|
| 멋쟁이사자처럼 AI스쿨 12주차 회고 (0) | 2023.03.09 |
| 멋쟁이사자처럼 AI스쿨 11주차 회고 (0) | 2023.03.02 |
| 통계 특강5 (0) | 2023.03.02 |
| 통계 특강4 (2) | 2023.03.01 |




댓글